Course content > MacroModels > Solids
Prerequisites
From our analysis of normal, tension, and friction forces, we know that normal solid matter compresses or extends in response to forces pushing on it, just like a spring. We would like to extract a parameter for a solid that is like the "density of a spring constant" -- the part of the spring constant for matter that is dependent only on the kind (and state) of matter we have, not on the specific object. In this section we figure out how to define (and measure) that parameter -- the Young's modulus of the material.
|
It is possible to push or pull on an object along just one direction. If you apply a force pressing into the object, we expect it to compress the object (shrink it), while if you pull away from the object (tension) we expect it to lengthen the object.
When an object is pulled or pushed in one dimension, we expect it to act like an elastic spring (at least for small deformations) and therefore to be well described by Hooke’s law:
F = k ΔL
We choose signs so that a positive applied force, F, is a tension that causes the object to increase its length, (ΔL > 0). A negative applied force is a compression that causes the object to decrease its dimension ((ΔL < 0). The proportionality factor is its spring constant, k.
|
 |
Stress and strain
To extract a parameter that is independent of the particular object we are considering but is only a property of the material (like a density), we have to decide how we think the result will depend on the particular object.
|
Consider what would happen if we had two blocks right next to each other and brought them together to create a single larger block with twice the force on it. Since each block stretched the same, we therefore would expect that the double block would stretch the same as the single block would if the force on the double block was double that of the force on the single block.
It therefore looks like what matters for the general block of material is the ratio of the force to the area. This makes sense if we think about individual atoms in the material. They don't know how big the object is, only how much force they individually are feeling. So in a molecular description, it would be the "force per atom" that would matter.
|

|
Since we are not looking for something we can use with macroscopic matter, we'll consider the parameter we want to explore as the stress -- the force per unit area. This is often represented by the Greek letter sigma (σ).

|
Now how about the object's response to the force? The object will respond by deforming, increasing or decreasing its original length, L0, by ΔL. If we took two blocks and put them on top of each other, we can analyze the long block by cutting it in half. We know from our standard N2/N3 arguments that the force the top and bottom halves of the long block would exert on each other would also be F. So if each separate block shrinks by a length Delta L, we expect the double length block would shrink by twice that.
This suggests that the relevant variable that is independent of the object's size is the fractional change in the total length (L0). This is called the strain and is often represented by the Greek letter epsilon (epsilon).

We can now look at the "Hooke's law type of force vs stretch" relationship in terms of a relation that tells about the material in general, and not about a specific block.
|
 |
|
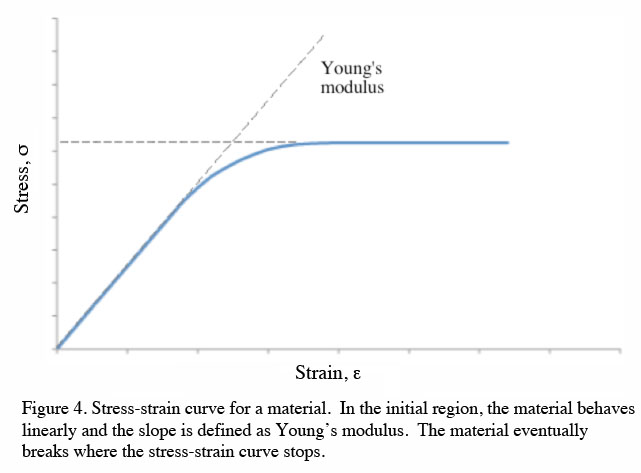
If the material responds elastically to the stress, there will be a linear region where stress is proportional to strain, such that

In this case, E is the slope and is called Young’s modulus of elasticity, though it is also called the elastic modulus or the stiffness. The steeper the slope, the stiffer the material.
|
 |
Shape dependence of the spring constant
We can now pull apart the spring constant in Hooke's law into a part depending on the size of the object and an intrinsic property of the material. If we write the force in terms of the stress, the stretch in terms on the strain, and then use Young's modulus, we can solve for the spring constant:

This shows how the spring constant for a uniform block of matter can be expressed in terms of a property of the material -- E -- times parameters of the specific object's shape. This is like a density, but because the force is applied along a particular direction, the dimension of the object along the direction of the force and perpendicular to it come in differently.
Young's modulus in biological systems
Note that in biological systems, stiffer ("stronger") is not always better. Materials such as arterial walls are ideally elastic (or less stiff) to respond to the increased pressure as blood is pumped around the body by the heart. However, stiff bones and stiff enamel on teeth are best as they give our bodies strength.
Forces are often applied along one critical dimension in an object or organism. This can result when animals try to move or when plants try to remain stationary. Forces can result from part of an organism being compressed, e.g when an antelope runs it uses its leg to push on the ground and propel it forward. Forces also result when something is stretched in tension, as when a spider suspends itself by a thread. Bending forces can result, when a tree branch is weighted down by snow.
Biological organisms use a lot of different materials to resist such forces and provide strength. Some examples include silk that makes up spider webs and silk moth cocoons, collagen that makes up our tendons and holds our skin together, chitin that makes the exoskeletons of arthropods, and cellulose, the fibrous material holding plants together. These materials often take the form of long fibers that help a structure to be strong along one particular dimension.
Young’s modulus, E, can be used to describe how  a material responds to a force. Because biological materials are not isotropic, the response to force can differ in different directions and may differ along the same direction for compression vs tension. Bones are often strongest along their length as a result of the collagen fibers that preferentially run along that axis. Bones have a larger elastic modulus in compression (18.5 GPa) than in tension (17.3 Pa; Wainwright table 5.5*). Bones typically respond elastically to force over a small range and then rapidly extend and break.
a material responds to a force. Because biological materials are not isotropic, the response to force can differ in different directions and may differ along the same direction for compression vs tension. Bones are often strongest along their length as a result of the collagen fibers that preferentially run along that axis. Bones have a larger elastic modulus in compression (18.5 GPa) than in tension (17.3 Pa; Wainwright table 5.5*). Bones typically respond elastically to force over a small range and then rapidly extend and break.
Skin has a very different response to stress. Skin is made up of collagen fibers in a matrix, in which are also embedded elastin fibers. Skin is typically always stretched over a body such that if it were removed it would shrink to shorter dimensions. This is the result of the elastin fibers that are kept in tension. As skin is pulled, it responds elastically based on the elastin fibers, until the point at which the collagen fibers start to be stretched. At that point, the skin becomes resistant to additional stretching. The stress strain curve of skin therefore looks very different from that of bone.
* S. A. Wainwright, Mechanical Design in Organisms, (Princeton U. Press, 1982)
Karen Carleton and Joe Redish 10/20/11
Comments (0)
You don't have permission to comment on this page.