Class content > Energy: The Quantity of Motion > Kinetic energy and the Work-Energy Theorem  > Energy of place -- potential energy

Prerequisites

• Coulomb's law
• Reading the content in the Work-Energy theorem  
• Energy of place -- potential energy 
• What do I actually have to know about integrals?

The idea of potential energy is that by changing the relative position of two objects, their kinetic energy can be changed in a reversible way as a result of the forces between objects. When this happens, we can define a "potential" energy -- an energy of place that can serve as a way to "store" energy.

With electrical forces, consider two identical + charges approaching each other in vacuum with equal and opposite velocities. As they approach, they each feel a force, slowing each other down. Eventually, they come to a stop (instantaneously), turn around, and are repelled back, speeding up. The kinetic energy in the system is drained by the forces, being replaced by the "energy of place" -- by the fact that the charges are close to each other. The forces between the charges then push them back, restoring the kinetic energy of the charges. Since the "draining" of the KE was reversible, we expect that the work done by the electric force between the charges can be expressed as a potential energy.

Work done by the electric force

The electric force is a bit more complicated than our other two examples (gravity and springs). Since the force between two charges falls of like 1/r², we can't treat it as a constant (like we could with gravity) and we can't treat it using a simple average (like we could with a spring). We have to do the integral explicitly. In order not to make things too messy, we'll set it up as simply as possible physically so the integral looks like something you've seen in calculus. And we'll see that dimensional analysis gives us almost the entire result anyway.

Let's consider a physical system made up of two positive charges.  We'll nail one down and consider the work done by the force of that charge, QB, on a second charge, QA, that's allowed to move. We'll put the fixed charge (labeled B) at the origin, and let the movable charge (labeled A) move along the x axis. Charge B exerts an electrical force on charge A. How much work does that force do as charge A moves?

From Coulomb's law, and since the distance between the two charges is x, we can see that if we move the charge A out by a distance Δx, the work done will be

Since the magnitude of the force is changed continually -- and not linearly, we really have to do the integral. So we just make the Δx really small, call it dx, and integrate:

We are just adding up the little bits of work done by the electric force on charge A as it moves out from an initial position x_i to a final position x_f. (Remember that the integral symbol is a stretched "s" standing for "sum".) 

We only have to do the integral of x^-2dx. Our simple rules for the integrals of powers tell us that the integral of xⁿ is xⁿ⁺¹/(n+1) so for n = -2 we get

and when we put in our initial and final positions we get

(Be careful to follow the signs through carefully. There are a lot of minus signs and more to come!)

Electric potential energy

Putting the result of our integration into our definition of work, we can see that the work only depends on the starting and ending values, so we can define a potential energy that is a function of x, U(x):

So by comparing the first and second lines, it's clear that we should identify our electric PE between two charges, Q_A and Q_B as

where we have been explicit to note that U_elec is a function of the separation x. Now this is for the special case of one charge nailed down and the axis x. We can make this more general by realizing that it's not the coordinate that matters here -- that was only to make the integral look simple. What matters physically is the distance between the two charges. It doesn't really matter that the other charge is nailed down. If they are both moving we have to pick a particular instant to consider, but at that instant the PE will still look the same.

We then have the general result for the electric PE between any two charges:

where r_AB is the distance between the charges A and B.

Dimensional analysis

We could have guessed this result from dimensional analysis. Since the electric force looks like kQQ/r² and since the work just multiplies by a distance, we might have guessed that we would get kQQ/r.  We couldn't have told that there would be no extra constant out front, though, without having done the integral.

Negative Energy?

When we worked through the derivation of electric potential energy, you might have noticed that we conveniently chose two positive charges (or two like charges) to consider. What would happen now if we considered two opposite charges in our analysis? As we saw in the forces discussion, our mathematical expression would not look any different because the sign of the charge is inside the Q_AQ_B. (Recall that an algebraic symbol is a container for a value, and that value can be positive or negative. When we have a negative charge, the "negative" is a part of the symbol -- not expressed explicitly out front.)

But what happens when we think about tracking the energy? Let's first re-consider the case above -- two identical positive charges starting out with some kinetic energy and zooming toward each other -- and track the kinetic energy as it changes to electric potential energy. We know that they start out with some kinetic energy, and as they get close together they slow down due to the electric force that repels them from one another. We also know from our energy analysis that this electric force results in a positive potential energy. Then as they slow to a stop and reverse direction, we see the kinetic energy build back up.

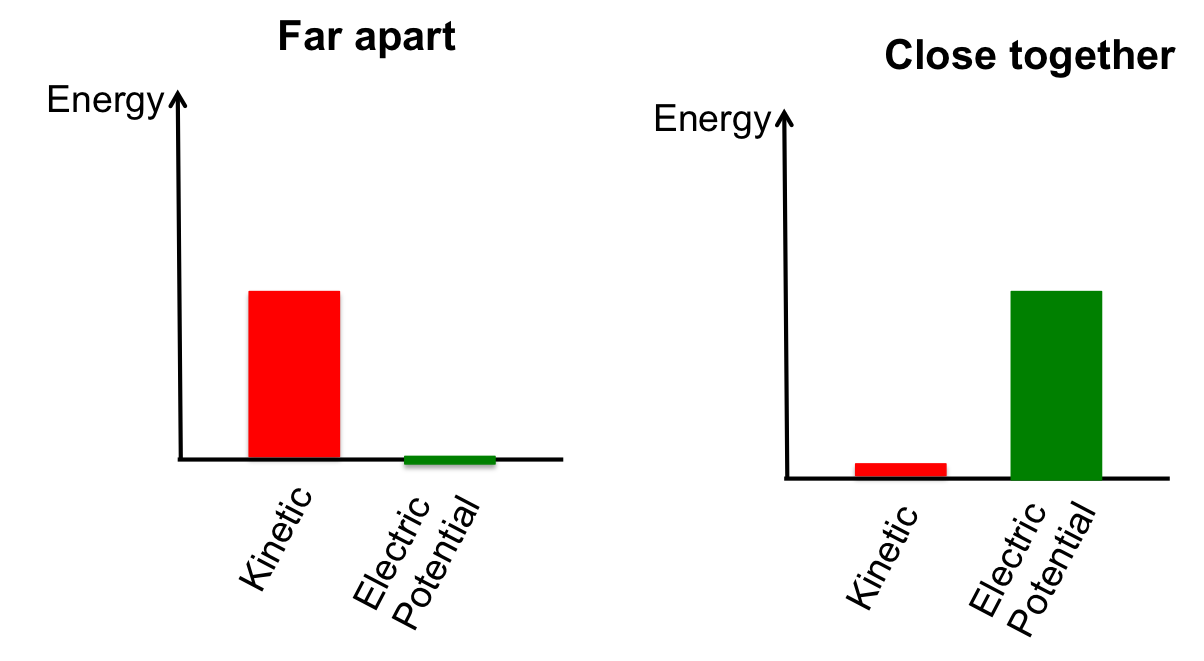
The mechanical energy (kinetic plus potential) here is conserved. The size of the kinetic bar when the two charges are far apart is the same as the size of the potential bar when they are close together and (instantaneously) stopped).

What would happen if we flipped the sign of one of the charges? Looking at the mathematical expression, we see we'd get a negative electric potential energy. We also know that with two opposite charges moving closer to one another, they wouldn't slow down - they would speed up! So we must have a way of representing the difference between have two like charges coming close to one another and having two opposite charges coming close to one another. One way we deal with this is by expressing the electric potential energy between two opposite charges as being negative energy. 

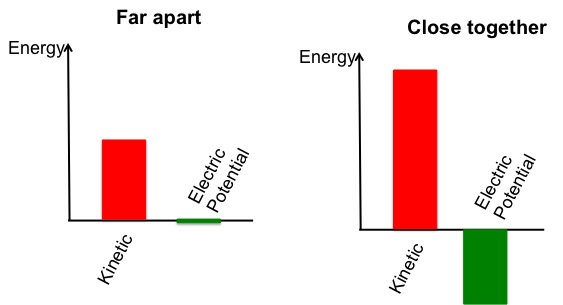
This is what we get if we just use our formula constructed from the positive charge example. When the two charges are far apart, the energy is purely kinetic. As they come closer and speed up the potential energy goes negative so the sum of the KE and PE stays the same even though the charges increase their speeds as they get closer. This leads to a result that is consistent both with what we know happens physically and with the equation of mechanical energy conservation. We will explore many implications of this in the units to come on chemical bond energy.

Joe Redish 11/3/11

Vashti Sawtelle 11/19/12