Working Content > Electric Currents
Prerequisites:
(Not required, but useful analogies)
When we have moving charge, we'll quantify how much is moving in the same way that we quantified fluid flow -- by counting how much passes a surface in a given amount of time. In order to be explicit, let's talk about electrons moving in a wire.
We'll assume that the electrons are always balanced by an equal and opposite density of positive ions, so the wire remains neutral even though the electrons are moving within it. If this were NOT the case, there would be a build up of charge someplace and this would take energy and complicate our discussion. This does in fact happen -- say in a capacitor, or when a wire is broken and current stops flowing, but the concepts we are developing (capacitance and resistance) allow us to separate these events. For our discussion of current, we assume that for any segment of the wire, as many electrons come in as go out in any unit of time.
|
 |
Definition of current
For a given wire, we'll define the amount of electric current in the wire by imagining a surface cutting the wire. We then ask, how much charge crosses that surface per unit time? In equations, this is:

where I is the amount of current flowing in the wire, and Δq is the amount of charge crossing the surface in a time Δt.
Note that we have charge crossing the surface even though the wire is neutral. This is because although there is a balance of positive and negative charges, only the negative electrons are crossing the surface. The positive ions stay fixed.
The dimensionality and units of the current is pretty straightforward. The dimensionality is just
[I] = Q/T
Current is a charge divided by a time. We define the natural unit, Coulomb/second as an Ampere.
1 Ampere = 1 Coulomb/second.
The problem of signs
One aspect of electric current that is often confusing is the question of the sign. Since we can have both positive and negative charges moving -- and in both directions -- it is convenient to include a sign in our current. Here's the way it works:
- We pick a direction in the wire that we designate as positive.
- We pick a surface crossing our wire that specifies the position at which we want to measure out current.
- If we have positive charges crossing the surface moving in the positive direction we designate that as a positive current.
- If the direction reverses we put a minus sign.
- If the sign of the charge reverses we put a minus sign.
You might have picked up on a confusing element here. If we have negative charges crossing our surface moving in the negative direction, this corresponds to a positive current! Yes, this is the way we do it and it does work out OK. This is illustrated in the figure below.
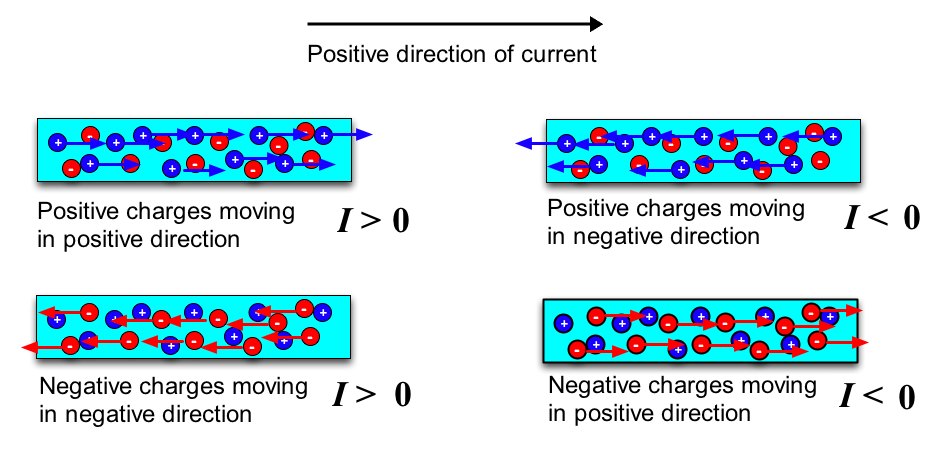
When we are analyzing electric circuits, you might get distressed because you don't know before you solve the problem which direction the charge is moving. Don't worry about it! Pick a direction and call it positive. If you picked wrong, your algebra will tell you by telling you that the current is negative -- going in the other direction!
Here's an animation that shows how electrons (red) might be thought of as moving through a metal with fixed positive ions (blue).

Connection to the microscopic model
It's useful to connect our definition of current to a model of individual moving charges. We do this in a way very similar to the way we analyzed the motion of molecules in an ideal gas.
Let's assume that we have a current of charges (and we'll treat them as positive for simplicity) moving to the right as shown in the figure at the right. (For clarity, we are not showing the stationary opposite charges that are balancing them.) And let's consider those crossing a surface with an area, A, as shown.
|
 |
How much charge crosses the area A in a time Delta t? Let's suppose that
- each moving charge making up the current has a charge, q
- the density of moving charge per unit volume is n
- the speed of the moving charges are v
Any moving charge that is less than a distance Δx = vΔt from the surface A will make it through before the end of our time interval. If it is farther back, it won't make it. Therefore, all the charges in the volume AΔx will make it through in the time interval. So:
- volume that makes it through = AΔx
- number of charges in that volume that make it through = nAΔx
- amount of charge that makes it through = qnAΔx
So the current is equal to the amount of charge that makes it through in a time Δt divided by Δt.
I = (qnAΔx)/Δt = qnvA
A useful construct is the amount of current per unit area that is flowing. We call this the current density, J.
J = qnv.
(Sometimes J is taken to be a vector in the direction of v. Then, to get back a current, you have to take a dot product with the vector of the area.)
Comment on randomness
Although we have described the charges in a current as moving with a uniform velocity, really, because of thermal motions, the individual charges' velocities actually vary randomly. Normally, the velocities of atoms, molecules, and electrons will average to 0. In the case when they are moving (say, due to an electric force), their velocities will be biased in the direction of the force and there will be a non-zero average velocity called the drift velocity. (Of course, for electrons in a metal, this is more complicated to describe accurately and requires quantum mechanics.)
Follow-ons:
Joe Redish 2/25/12
Comments (0)
You don't have permission to comment on this page.